


Next: Examples of Wavelets
Up: The Wavelet Transform
Previous: Introduction
The Morlet-Grossmann definition of the continuous wavelet
transform [17] for a 1D signal
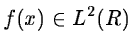 is:
is:
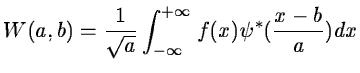 |
|
|
(14.1) |
where z* denotes the complex conjugate of z, 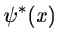 is the
analyzing wavelet, a (>0) is the scale parameter and b is
the position parameter. The transform is characterized by the
following three properties:
is the
analyzing wavelet, a (>0) is the scale parameter and b is
the position parameter. The transform is characterized by the
following three properties:
- 1.
- it is a linear transformation,
- 2.
- it is covariant under translations:
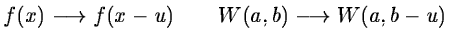 |
|
|
(14.2) |
- 3.
- it is covariant under dilations:
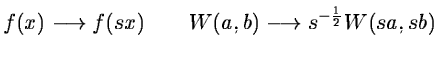 |
|
|
(14.3) |
The last property makes the wavelet transform very suitable for
analyzing hierarchical structures. It is like a mathematical
microscope with properties that do not depend on the magnification.
In Fourier space, we have:
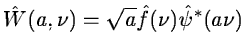 |
|
|
(14.4) |
When the scale a varies, the filter
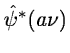 is only reduced or
dilated while keeping the same pattern.
is only reduced or
dilated while keeping the same pattern.
Now consider a function W(a,b) which is the wavelet transform of a
given function f(x). It has been shown
[#grossmann<#14252,#holschn<#14253] that f(x) can be restored using the
formula:
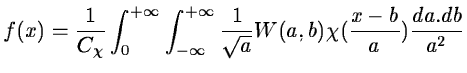 |
|
|
(14.5) |
where:
 |
|
|
(14.6) |
Generally
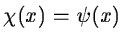 ,
but other choices can enhance certain features
for some applications.
,
but other choices can enhance certain features
for some applications.
The reconstruction is only available if 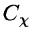 is defined (admissibility
condition). In the case of
is defined (admissibility
condition). In the case of
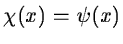 ,
this condition implies
,
this condition implies
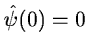 ,
i.e. the mean of the wavelet function is 0.
,
i.e. the mean of the wavelet function is 0.



Next: Examples of Wavelets
Up: The Wavelet Transform
Previous: Introduction
Petra Nass
1999-06-15
![]() is:
is:
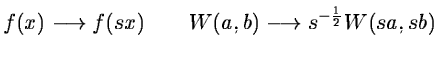
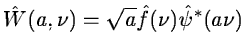
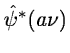 is only reduced or
dilated while keeping the same pattern.
is only reduced or
dilated while keeping the same pattern.
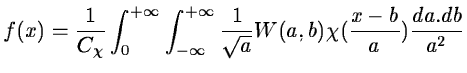

![]() is defined (admissibility
condition). In the case of
is defined (admissibility
condition). In the case of
![]() ,
this condition implies
,
this condition implies
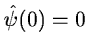 ,
i.e. the mean of the wavelet function is 0.
,
i.e. the mean of the wavelet function is 0.