gnuplot's interactive environment has many features that make it easy to use. In this section you will learn about some of these features.
gnuplot provides very detailed online help for all commands. The entries
in the online help are identical to those you find in the gnuplot manual.
To access the help facility, simply type a question mark (?) or
help at the
gnuplot> prompt. To get help on a particular command, type ?
![]() command
command ![]() . If you are using the DOS version and can not access
the online help, please read the README file and check to make sure that
gnuplot is properly installed on your PC.
. If you are using the DOS version and can not access
the online help, please read the README file and check to make sure that
gnuplot is properly installed on your PC.
gnuplot has a mechanism that allows you to recall previous commands and edit them. On the PC, the up/down arrow keys are used to get the previous/next commands. The Home, End, and left/right arrow keys are used to move the cursor around (the Home and End keys move the cursor to the beginning and end of the line, respectively.). On Unix, the arrow keys can be used if you have the correct terminal setting. Otherwise the Emacs control sequence can be used (e.g., ^p for previous command, ^n for next command, ^b to move left one character, ^f to move right one character, ^d to delete a character, etc.).
Another nice feature of gnuplot's command line is that it will accept abbreviations of commands and keywords as long as they are not ambiguous. For example, replot can be abbreviated as rep, parametric as par, linespoints as linesp, etc. While this is handy for interactive gnuplot sessions, it may not be a good idea to abbreviate commands in script files (to be discussed later) because it make the commands less comprehensible.
You should familiarize yourself with the arithmetic and logical expressions in gnuplot. Basically, they are similar to Fortran and C expressions, e.g. ** for exponentiation, && for logical AND, || for logical OR, etc. For details on the complete set of operators, refer to the gnuplot manual.
If you use some constants or functions repeatedly in your work, you
might find it convenient to give them names that are easier to
remember. For example, if you use the constants ![]() and
and
![]() very often, you can name them in gnuplot by
very often, you can name them in gnuplot by
mu=10.98765 sigma=6.43321Now suppose you want to plot the function
plot 1/(sqrt(2*pi)*sigma)*exp(-(x-mu)**2/(2*sigma**2))You may find typing the above function cumbersome, especially if you need to use it several times. gnuplot lets you do this:
f(x,mu,sigma)=1/(sqrt(2*pi)*sigma)*exp(-(x-mu)**2/(2*sigma**2))(You could leave the mu and sigma out of the argument list if you don't need to vary them.) You can now do things like
plot [-5:15] f(x,6,1),f(x,3.5,2)Numbers without decimal points are treated as integers rather than as reals. Expressions using only integers are evaluated by integer arithmetic. Thus 1./4. = 0.25, but 1/4 = 0. This can lead to wrong results if you are not careful.
Being able to define custom functions has a few advantages other than saving typing. Here is a handy trick: suppose you have the following function:
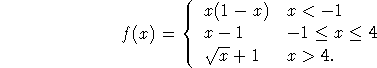
Defining this function in gnuplot can be done by stringing a few functions together:
f1(x)=(x<-1) ? x*(1-x) : x-1 f2(x)=(x<=4) ? f1(x) : sqrt(x)+1These function definitions may look strange to you if you are not familiar with the ternary operator
Note that although the function above is defined differently in three intervals, it is continuous at the boundaries of those intervals. If the function is not continuous at the end points of the intervals, gnuplot will still connect the endpoints. If you want to plot a discontinuous function, you'll need to define it in separate pieces and plot them together. The trick is to set the unwanted sections equal to something unprintable (no, this isn't x-rated), such as
f(x)=(x<0) ? cos(x) : sqrt(-1) g(x)=(x<0) ? x/0 : sin(x)This obviously would work for a continuous function as well. (It wouldn't work at all if gnuplot were unfriendly enough to crash upon encountering mathematical no-no's.)
One other interesting use of the ternary operator is that it can be used to approximate the definite integral of some function. The example below is taken from the demo file bivariat.dem which is included in the gnuplot distribution.
# integral2_f(x,y) approximates the integral from x to y. # define f(x) to be any single variable function # # the integral is calculated as the sum of f(x_n)*delta # do this (y-x)/delta times (from y down to x) f(x) = exp(-x**2) delta = 0.02 # If you're running under MS-DOS, use delta = 0.2 # integral2_f(x,y) takes two variables; x is the lower limit, # and y the upper. Calculate the integral of function f(t) # from x to y integral2_f(x,y) = (x<y)?integral2(x,y):-integral2(y,x) integral2(x,y) = (x>y)?0:(integral2(x+delta,y)+delta*f(x))Note that f(x) is defined as
plot f(x),integral2_f(-10,x)
There is a command, print, which will evaluate an expression and print the result on the screen. For example, try the following:
print cos(pi) print exp(-0.5*(1.96)**2)/sqrt(2*pi)One implication of this is that you can use gnuplot as a calculator.
Sometimes you will want to use the same set of commands many times. gnuplot allows you to put those commands in a script file and load the file into gnuplot. You can use a text editor (such as Emacs, vi, or Norton Editor) to create or edit such a file. Once you have created the file, you can run the commands in that file in two ways. First, you can run gnuplot and use the load command to run the commands in the script. The other way is to run the script in batch mode by typing the filename of the script as the command line argument to the gnuplot command. For example, to run the script called myplot.gp in batch mode, type
gnuplot myplot.gpThis will invoke gnuplot. After it finishes executing the commands in the script, it exits, and you are back to the system command prompt. (There is a pause command, which will be discussed later.) This is convenient if you want to output plots to some graphics file instead of viewing them on the screen.
A few special characters are very useful in script files. Everything after
a number sign, #, on a single line in a script (or, for that matter, on
a command line) is treated as a comment and is ignored by gnuplot.
The continuation character is the backslash, ![]() . Multiple
commands can be placed on a single line if you separate them by a
semicolon, ;.
. Multiple
commands can be placed on a single line if you separate them by a
semicolon, ;.
Suppose you have defined some variables and functions and customized some settings with the set command. If you want to keep all these so that you can use them later, you can write all these (along with all of the default values you have not set and the last plot or splot command) to a file by
save 'mystuff.gp'The filename and extension are arbitrary, of course. If you only want to save the functions you have defined, you can use
save function 'myfunc.gp'The same applies to variable and set.
To load the file into gnuplot, use the load command. For example:
load 'mystuff.gp'
Included in the gnuplot distribution, along with demo files, is a file named stat.inc, which contains definitions of many cumulative distribution functions and probability density (or mass) functions for many continuous and discrete distributions. To access these functions, you can do load 'stat.inc'. The demo files prob.dem and prob2.dem show how these functions can be used.